It makes some intuitive sense that a taller man would have a bigger penis. After all, taller men tend to have longer legs and bigger hands and larger heads, why wouldn't his penis also be large? It seems so obvious that it's become part of the assumed cultural knowledge: tall guys must have big dicks.
And if there's anything scientific researchers love to do, it's examining the truth behind assumed cultural knowledge. There have been many penis size studies over the years, and more than a dozen looked at the relationship between penis size and the rest of the man's body measurements (in scientific parlance, somatometric parameters). And while results have varied, no study found a clear and obvious relationship between height and penis size. Let's dive in.

Standard deviations
Before we get started, we need to define some terms that will be useful in this examination. The first is "standard deviation". This is a measurement of how widely the data is dispersed in relation to the mean (average). A standard deviation only works when the collected data has a normal (bell curve) distribution, which it turns out both height and penis size fit rather nicely. Most folks are near average, some are more or less, and only small groups are significantly far from the average.
Standard deviations (SD) break the population into segments. 1SD above the mean accounts for 34.1% of the population, as does 1SD below. The second SD band above and below the average add less than half that at 13.6%. The 3rd SD groups are just 2.1%. Beyond that is 0.1% on either end of the bell curve. The size of the SD didn't change, just the area under the curve.
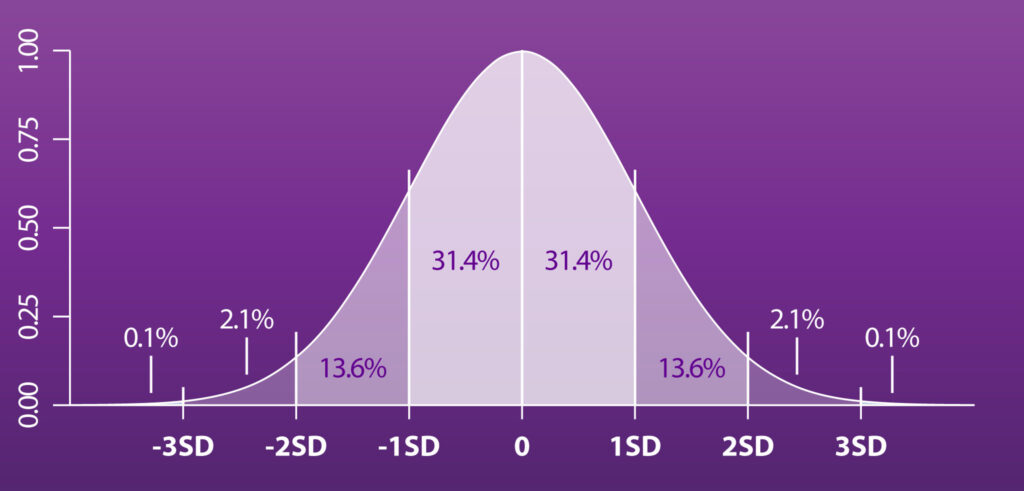
The larger a standard deviation is, the more broad the bell curve and the more data points you'll find further from the average. Conversely, a smaller SD means a tighter bell curve with most of the data clustered near the average.
According to data from the US Centers for Disease Control, the average adult male American is 5 feet 9.3 inches (1.75 meters), with a standard deviation of 2.94 inches (8.47 cm). That means that 68% of men are between 5' 6" and 6' 0" (1.67 and 1.84 meters). This majority of men are all within 4% of the average height.
(American height data was chosen because it is among the most comprehensive available and the ethnic mixture of the American population is a halfway decent proxy for the rest of the world)
Meanwhile, the average penis is 5.5 inches (13.98 cm) long with a standard deviation of 0.68 inches (1.72 cm). So with that same bell curve, you'll find that 68% of penises measure between 4.82 and 6.18 inches (12.24 to 15.7 cm) — a 10.5% range on either side of average.
It turns out there is much greater distribution in penis sizes than there is in height. That must be because penis size increases with height, right? Not so fast.
Pearson's coefficient
The other term we need to know is the Pearson's correlation coefficient. This unitless measurement is an examination of how closely related two values are across a population. The further the number is from 0, the stronger the relationship between A and B. If a dataset is found to have a correlation coefficient of 1, it's a perfect positive relationship — as X increases, so does Y. Conversely, a coefficient of -1 means that X increasing means Y decreases. While a coefficient of 0 means there is no relationship between the two measurements.
A good example of the Pearson's coefficient is in infants. The larger the measurement of the baby's height, the heavier you can expect the baby to be. But the baby height/weight correlation not a perfect 1, since some infants are simply fatter than others. But it's still a strong correlation, and one that is obvious.
The coefficient can be visualized by how closely the points on a scatterplot graph hew to the linear regression line (best fit) of that data. The closer the points are to the line, the stronger the correlation and the further from 0 the coefficient will be. A weaker relationship will be shown by points that are scattered further from the line and a score that's closer to 0.
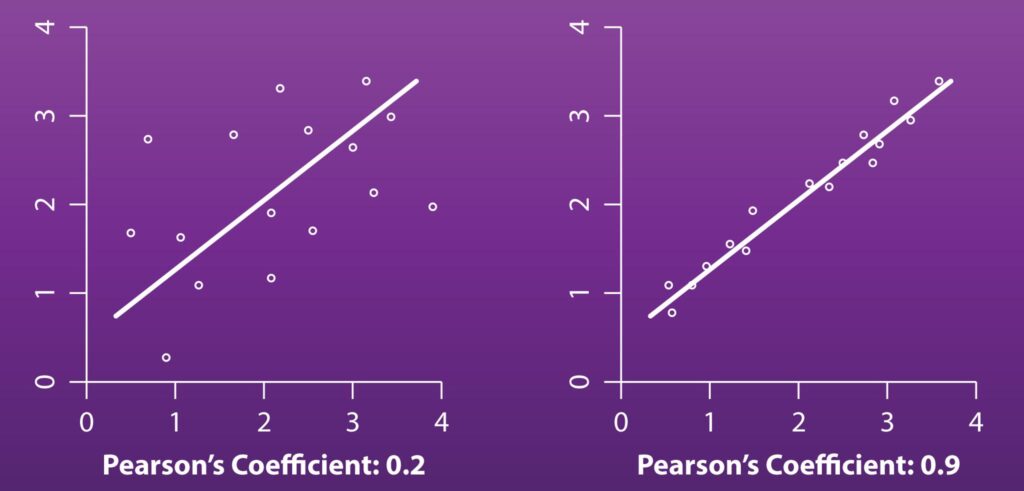
A set of widely dispersed data points and one of an obviously tight relationship can result in the same linear regression line — the coefficient is a measure of how closely to that line you can expect any point to land.
In general, a Pearson's coefficient measuring between -0.3 and 0.3 is generally considered weak, one between 0.3 and 0.5 (or -0.3 and -0.5) is a moderate correlation, while anything greater than 0.5 or less than -0.5 is viewed as a strong correlation.
Penis Size & Height Correlation
More than a dozen studies around the world have examined the relationship between height and penis size, producing a Pearson's coefficient to show just how closely related the two measurements are. Only two found what would qualify as a "moderate" correlation, and not by a wide margin. Roughly one third saw a weak correlation, and half reported no correlation or a coefficient so close to zero it barely counts.
Here they all are, ranked from strongest correlation to weakest:
| Study | Pearson's Coefficient |
|---|---|
| Acuña 1999 | 0.33 |
| Mehraban 2007 | 0.307 |
| Promodu 2007 | 0.25 |
| Nasar 2011 | 0.240 |
| Park 2016 | 0.211 |
| Choi 2011 | 0.185 |
| Aslan 2011 | 0.164 |
| Awwad 2011 | 0.05 |
| Chen 2014 | 0.049 |
| Shalaby 2014 | -0.013 |
Additionally, both Söylemez 2012 and Spyropoulos 2002 reported "weak" correlations between height and penis size, but did not provide a specific coefficient value. Granados-Loarca 2005 and Rad 2020 stated that they found no correlation without providing a coefficient value, but it can be safely assumed that it was very near zero. There are dozens of other penis size studies, but only these offered Pearson's correlation coefficients for height.
So at best, we have a barely "moderate" correlation, but in general any correlation that was found was fairly weak to nonexistent.
But what are you supposed to do with this coefficient number?
Height is a poor predictor of penis size
The Pearson's coefficient is at its core an examination of the relationship between the standard deviations of two datasets. The closer the coefficient is to 1, the closer you are to a change of 1SD in measurement X resulting in 1SD change in measurement Y. In essence: ΔSDX × Coefficient = ΔSDY
To give the theory of height influencing penis size the best shot, we'll use the strongest correlation found: 0.33 from Acuña 1999. With that, our height SD of 2.94 inches (8.47 cm), and our penis length SD of 0.68" (1.72 cm), we can judge that every 1 SD change in height can be predicted to result in a 0.33 SD change in penis size: every 3 inches (7.6 cm) in added height is only predicted to add 0.23 inches (6 mm) in penis length.
That also works out to a roughly scalar relationship, where a 10% increase in height (a very significant 6 inches / 15 cm) results in a 10% increase in penis size (a not very significant 0.5 inches / 1.3 cm). And that's using the study with the strongest correlation!
In reality, averaging these studies gets us a correlation coefficient of 0.177 — a rather weak relationship. With this, our relationship between height and penis size is basically halved:
Every 3 inches (7.6 cm) in added height is only predicted to add 0.12 inches (3 mm) in penis length.
But why is this? It seems like everything else about the body is correlated with height, why isn't the size penis? The things we can easily observe like hands, limbs, and heads, are all sized by their bones, and tall people simply have bigger skeletons. But the penis doesn't have any bones in it, so skeletal size has no impact on the size of the penis.
It might seem counterintuitive, but many internal organs also don't obey the idea of "bigger person = bigger organs". The heart and lungs will generally be larger on a tall person, as they must pump harder and oxygenate more blood to keep the body functioning. But other organs, like kidneys and pancreases tend to be more "one size fits all". Because the size of the penis has no bearing on the functioning of the rest of the body, it doesn't scale the same way the heart and lungs do with increasing body size.
Additionally, by not pegging genital size to body size, it allows for most tall and short men to still have average-sized endowments and for tall and short women to have average-sized vaginas — meaning that body size doesn't influence sexual compatibility.
The size of a man's body is a poor predictor of the size of his penis. The long and short of it is that most men, regardless of height, have average penises. And that's okay.











